“The principle of superposition” tells you that when waves are overlaid each other, the resultant displacement of each position becomes the summation of the individual displacement of each wave. The Fourier transform tells you that an arbitrary complex wave can be represented by the summation of a set of sinusoidal waves. Especially the resultant complex wave is periodic and its period is T [s] in time, each sinusoidal wave has the periodicity of T. The next figure explains this more in detail.
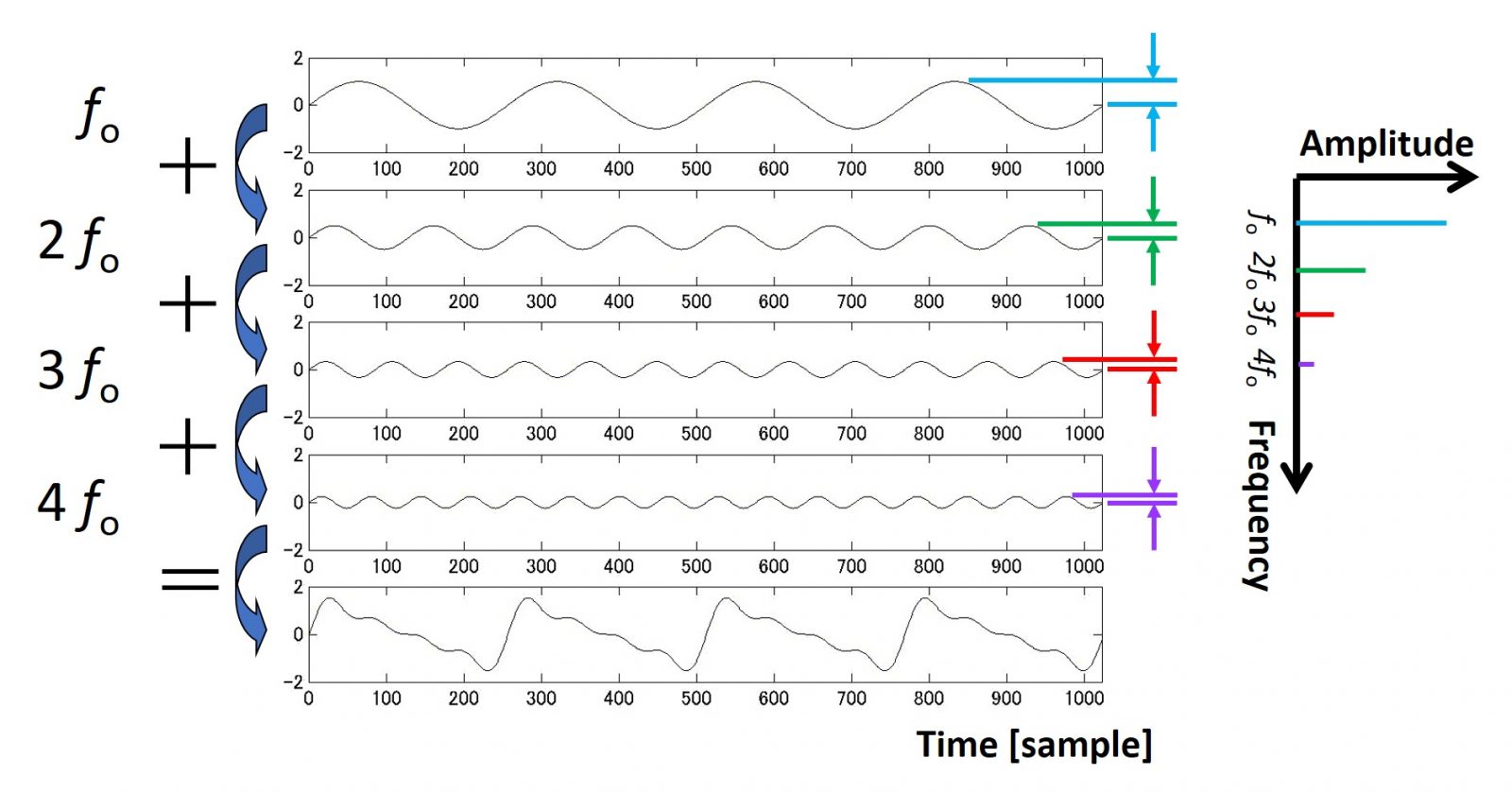
The first panel shows the sinusoidal wave with the frequency of fo. When you compare another sinusoidal wave in the second panel with the frequency of 2 fo, the second wave has its period half as long as the first wave, because the frequency is doubled. Likewise, when you compare the next sinusoidal wave in the third panel with the frequency of 3 fo, the third wave has its period 1/3 as long as the first wave, because the frequency is tripled. Finally, the fourth wave has its period 1/4 as long as the first wave, because its frequency is 4 times as high as the first wave. Thus, all the four sinusoidal waves have the common periodicity of T, and therefore, the complex wave in the bottom panel as the summation of all of four waves has the same periodicity with its period of T, which is called the fundamental period. Furthermore, the reciprocal of T is fo, which is called the fundamental frequency of the complex wave. In summary, a complex periodic wave is decomposed into a set of sinusoidal waves, of which the frequencies are always multiples of fo.
The right most part of the same figure shows how much each individual sinusoidal component is included in this complex wave in terms of its amplitude. Therefore, this plot is called the amplitude spectrum (as a function of frequency). Each bar (colored line) of this amplitude spectrum shows the maximum displacement of each sinusoidal wave at the frequency of multiples of fo. A set of such sinusoidal waves are called harmonics. Finally, the amplitude spectrum of a complex wave becomes a line spectrum in the harmonic structure, of which each line is located at the frequency of n fo.