Human beings are able to more or less independently control phonation (source) with the larynx and articulation (filter) with the vocal tract. Thus, we can assume speech sounds are the response coming from a vocal-tract system, where a sound source is fed into and filtered by the resonance characteristics of the vocal tract. This kind of modeling by a linear system is called the source-filter theory of speech production. For vowels, the sound source is a glottal sound produced by vocal fold vibration. The glottal sound governs pitch and voice quality. When the vocal-tract configuration changes, the resonance characteristics also change, and the vowel quality of the output sound changes.
When we talk about speech sounds, whether vowels or consonants, there are four sound sources: glottal (or phonation) source, aspiration source, frication source, and transient source. When we produce speech sounds, one of the sources or a combination of them becomes an input to the vocal-tract filter, and a vowel or a consonant can be viewed as the response of such filter. Thus, the source-filter theory can be expanded and applied not only to vowels, but to any speech sound, including consonants.
If the vocal-tract configuration is unchanged, the vocal-tract filter becomes a linear time-invariant (LTI) system, and an output signal $y(t)$ can be expressed by the convolution of an input signal $x(t)$ and the impulse response of the system $h(t)$, that is,
$$y(t) = h(t) \ast x(t),$$
where the asterisk denotes the convolution.
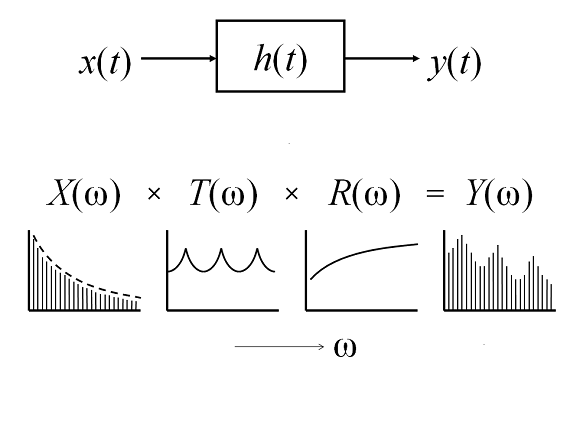
The equation above is expressed in the time domain, but it can also be expressed in the frequency domain as follows:
$$Y(\omega) = H(\omega) X(\omega),$$
and this tells you the relation of each spectral representation. In other words, the speech spectrum $Y(ω)$ is modeled as the product of the source spectrum $X(ω)$ and the spectrum of the vocal-tract filter $H(ω)$.
Strictly speaking, the spectrum of the vocal-tract filter $H(\omega)$ can be further viewed as the product of the vocal-tract transfer function $T(\omega)$ and the radiation characteristics from a mouth $R(\omega)$, that is,
$$Y(\omega) = [T(\omega) R(\omega)] X(\omega).$$
The spectral slope of $X(\omega)$ is approximately -12 dB / oct. (decreasing 12 dB when the frequency is doubled). The spectral slope of $T(\omega)$ is more or less flat, even though the vocal-tract configuration changes because of articulation. Finally, the spectral slope of $R(\omega)$ is approximately 6 dB / oct. As a result, vowels have the spectral slope of approximately -6 dB / oct.
Let’s take a look at a simple demonstration of the source-filter theory. In this demonstration we use an impulse train as a simple sound source with a flat spectrum. There are two sound sources with doubled fundamental frequencies. There are also two vocal-tract filters: one for vowel /a/ and the other for vowel /i/. By comparing all four combinations, the same sound source yields the same pitch contour, even though the vowels are different. Likewise, the same vocal-tract filter yields the same vowel quality, even though the pitch contours are different.
Filter /a/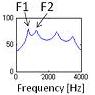 |
Filter /i/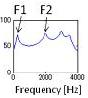 |
|
|---|---|---|
Source 1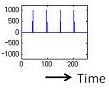
|
||
Source 2
|
Although the source-filter theory is a good approximation of speech sounds, we have to remember this theory is only an approximation, and the actual process of speech production is non-linear and time-variant. It is also true that there is an interaction between a source and a vocal-tract filter. When you need to discuss such issues in a strict sense, you might need to pay more attention. However, this theory usually gives us reasonable approximations, and therefore, many speech applications in speech technology are based on this theory.
The basic conception of source-filter theory appears in Chiba and Kajiyama (1941). These researchers explained the mechanisms of speech production based on the concept of phonation and articulation scientifically and systematically (Kasuya, 2001). Dr. Fant was trained in electrical circuit theory in 1944 and 1945 from a teacher who was an expert on filter theory. Then, Fant encountered “Chiba and Kajiyama,” perhaps when he visited Massachusetts Institute of Technology (MIT) (Fant, 2004; Arai, 2004). At this point, Chiba and Kajiyama’s view of phonation and articulation merged with Fant’s filter theory. It lead to the so-called “source-filter theory of vowel production” in modern acoustic theory of speech production (Fant, 1960), and this is one of the reasons that Chiba and Kajiyama is considered a classic in the history of science (Maekawa and Honda, 2001).
- Arai, T., “History of Chiba and Kajiyama and their influence in modern speech science,” Proc. of From Sound to Sense: 50+ Years of Discoveries in Speech Communication, 115-120, 2004.
- Chiba, T. and Kajiyama, M., The Vowel: Its Nature and Structure, Tokyo-Kaiseikan Pub. Co., Ltd., Tokyo, 1941.
- Fant, G., Acoustic Theory of Speech Production, (Mouton, The Hague, Netherlands), pp. 15-90, 1960.
- Fant, G., personal communication, 2004.
- Kasuya, H. et al., “Overview in each research field: Speech,” J. Acoust. Soc. Jpn., 57(1), 11-20, 2001.
- Kent, R. D. and Read, C., Acoustic Analysis of Speech, Singular Publishing, San Diego, CA, 2001.
- Maekawa, K. and Honda, K., “On the Vowel, Its Nature and Structure and related works by Chiba and Kajiyama,” J. Phonetic Soc. Jpn., 5(2), 15-30, 2001.
- Stevens, K. N., “The acoustic/articulatory interface,” Acoustical Science and Technology, 26(5), 410-417, 2005.