Let’s think of a spring mass system hanging from the ceiling, as drawn in the following figure. When we pull the mass downward and release it, the mass is set into simple harmonic motion. Let’s take a closer look at this.
When the spring is stretched and released, a restoring force occurs. The restoring force is proportional to the length of the extension and the mass. This is called Hooke’s law. The restoring force causes the mass to return to its original position, or equilibrium; however, because of the inertia of the mass, the mass passes beyond the point of equilibrium and reaches the maximal point. Again the restoring force occurs and the mass starts moving downward from the maximal point. Again, because of the inertia of the mass, the mass passes through the equilibrium and reaches the minimal point. The mass repeats the same cycle again and again.
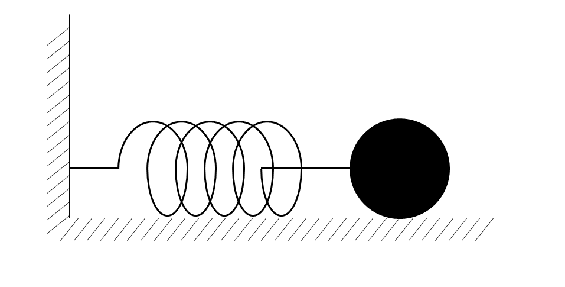
Let’s look at this simple harmonic motion in terms of the law of the conservation of energy. For this discussion, the spring-mass system rests on a surface, as shown in the following figure. In this system, the mass moves back and forth on the surface with no friction. When we pull the mass until the maximal point on the right, the kinetic energy is 0, but the elastic energy is the maximum. After releasing the mass, it moves back to equilibrium due to the restoring force. At this point, the elastic energy becomes 0, but the kinetic energy becomes the maximum. Because of inertia, the mass passes through the equilibrium and reaches the maximal point on the left, and at the maximal point, the movement stops for that instant. At this moment, again the kinetic energy is 0, and the elastic energy is maximal. Right after that, the mass moves again back towards the equilibrium. At the equilibrium, again the kinetic energy becomes maximal, and the elastic energy becomes 0. Thus, under the law of the conservation of energy, the energy alternates between elastic energy and kinetic energy within a cycle.
Now, let’s determine the period $T$ of the simple harmonic motion by the mass m and the spring constant k. Taking the x-axis horizontally, and given $x = 0$ at the equilibrium, the equation of motion in terms of the mass is
$${F} = -{ma} $$ where a is acceleration. On the other hand, Hooke’s law is
$${F} = -{kx} $$ where x denotes the displacement of the mass from the equilibrium, and the negative sign means that the direction of the restoring force by the spring is the opposite of the direction of the displacement of the mass. From the two equations above, we obtain
$${ma} = -{kx} $$ and therefore,
$${ma}+{kx} = 0 $$ Because acceleration is the second derivative of the displacement $x$ (in terms of time $t$), this equation is a differential equation. By solving this differential equation, the sinusoidal motion and the period $T$ can be determined by the formula:
$${T} = 2\pi\sqrt{ \frac{k}{m} }$$
Finally, the frequency, $f$, is the reciprocal of the period, $T$, that is,
$$f = \frac{1}{ 2\pi }\sqrt{ \frac{k}{m} }$$
Let’s think of mounting a pen at the mass to trace the simple harmonic motion. When a sheet of paper placed next to the pen does not scroll, the trace is a line segment. However, when we scroll the sheet of paper, the trace becomes a sinusoidal wave.
The prongs of a tuning fork also move in simple harmonic motion. When a tuning fork is place in the air, the surrounding air is compressed and then rarefied, and the sound wave propagates as a longitudinal wave. The following figure shows an image of sound propagation from the tuning fork. In this case, the sound pressure changes sinusoidally in time. This type of sound is called a pure tone, and it produces the sensation of a single pitch for us.
[References]
- Speaks, C. E., Introduction to Sound: Acoustics for the Hearing and Speech Sciences, Singular Publishing, San Diego, CA, 1999.