When a uniform tube has one closed end and one open end, a standing wave (resonance) can occur. In this case, the standing wave formed in the tube shows the following velocity distribution of air particles:
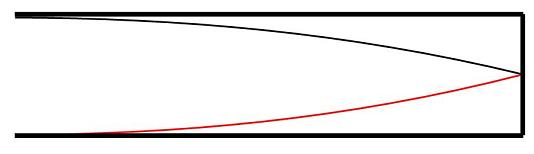
As shown in this figure, the node is located at the closed end, and the anti-node is located at the open end. This is because the closed end acts as the fixed end while the open end acts as the free end.
Now, let’s estimate the wavelength $\lambda$ in the above case. If the length of the tube is l, $\lambda$ is 4l because a quarter wave is formed in the tube, that is,
$$\lambda = 4l.$$
When the speed of sound is c, the frequency of sound, f, is
$$f = c /\lambda,$$
and therefore,
$$f = c / ( 4l ).$$
When c = 340 m/s and l = 17 cm,
$$f = c /\lambda = 340 / (4×0.17) = 500\mathrm{Hz},$$
therefore, the resonance frequency is 500 Hz.
The following standing wave can also be formed where a resonance occurs:
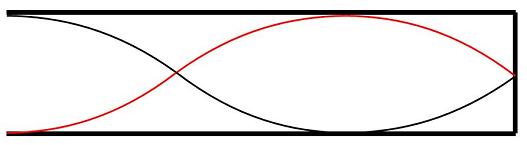
In this case, the wavelength $\lambda$ is 4/3 times as long as the length of the tube, l, that is,
$$\lambda = 4l / 3$$
and therefore, the frequency, f, is
$$f = 3c / ( 4l ).$$
Likewise,
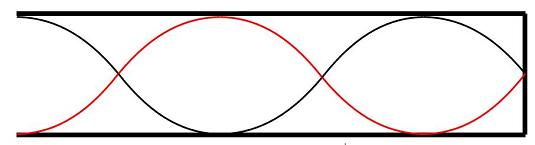
in the above case,
$$\lambda= 4l / 5$$
and the frequency, f, is
$$f = 5c / ( 4l ).$$
Finally, the resonance frequency fn is
$$fn = c / ( 4l ) × n \ (n = 1, 3, 5, \cdots).$$
When c = 340 m/s and l = 17 cm, the first three resonance frequencies are 500 Hz, 1500 Hz, and 2500 Hz.
Actually, air particles around the open end also vibrate. In other words, the effective length of the tube is a little bit longer than the actual tube length. The effective length depends on the radius of the tube r and,
$$\mathrm{the \ effective \ length \ of \ the \ tube} \fallingdotseq l + 0.6r.$$
This “open end correction” yields a better estimation of the resonance frequencies.
- Stevens, K. N., Acoustic Phonetics, MIT Press, Cambridge, MA, 1998.