Resonance occurs in a uniform tube, where one end is closed and the other end is open, when the frequency is an odd-number multiple of the fundamental. Perturbation theory tells us whether each resonance frequency increases or decreases (and by how much) when a small change occurs in the diameter at a local region of the tube.
Let’s take a look at the volume velocity distribution of air particles inside the tube when the standing waves with the first and second resonance modes occur.
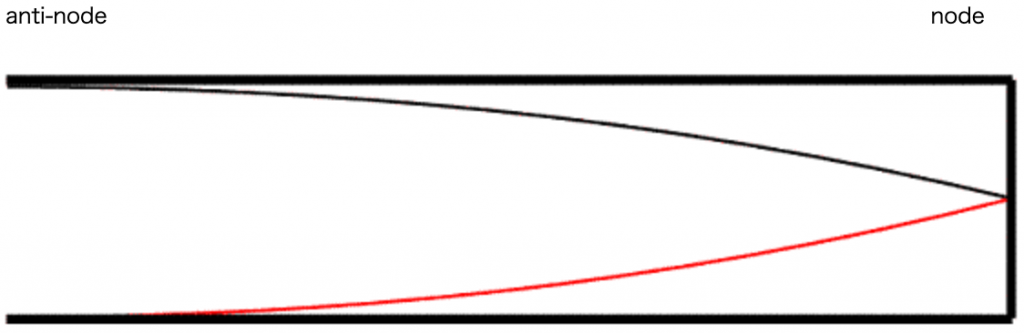
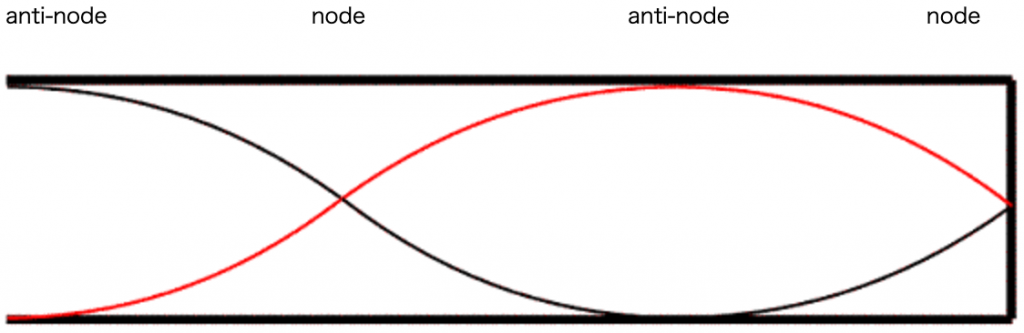
According to perturbation theory,
- the resonance frequency of the particular resonance mode decreases when a constriction is located at an anti-node of that resonance mode; and
- the resonance frequency of the particular resonance mode increases when a constriction is located at a node of that resonance mode.
From these facts, we can derive the following:
- all resonance frequencies decrease when the lips are rounded,
- the second resonance frequency decreases when a constriction occurs at the pharyngeal region because the second resonance mode has an anti-node in that region; and
- the second resonance frequency increases when a constriction occurs at the palatal region because the second resonance mode has a node in that region.
Thus,
- Vowel /i/: F2 frequency is higher because there is a constriction in the palatal region.
- Vowel /a/: F2 frequency is lower because there is a constriction in the pharyngeal region.
- Vowel /u/: F1 and F2 frequencies are both lower because there is a constriction at the lips.
A general approach to perturbation theory is based on a theorem by Ehrenfest (1916). Perturbation theory tells us the relationships between vocal tract configurations and formant frequencies by examining the changes in the formant frequencies that occur as a result of small perturbations of the area function in some region along the length of the vocal tract (Stevens, 1998).
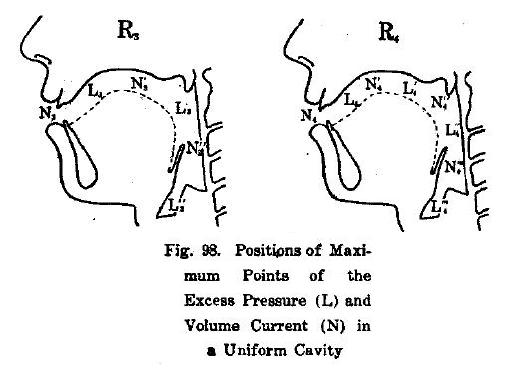
In chapter XI of “Chiba and Kajiyama” the researchers use their measurements to calculate the distribution of sound-pressure amplitude and velocity amplitude for the first two formants for different vowel configurations.(Fig. 96-98)
It is generally accepted that Chiba and Kajiyama showed the physical phenomenon of wave propagation in the vocal tract for the first time (Motoki, 2002).
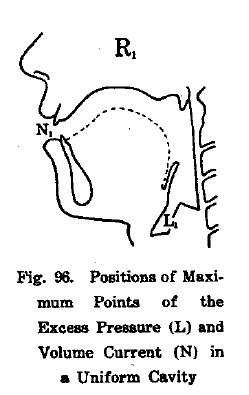
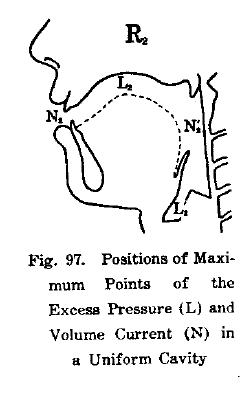
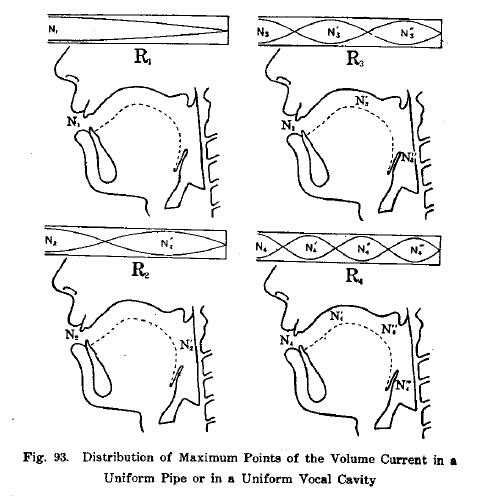
The relevance of their work was only recognized some decades later, though, when Stevens used such plots to predict the acoustic effects of perturbations on vocal tract shape (Stevens, 2001). Fig. 93 from “The Vowel” was cited by Fant and adopted by many subsequent monographs of acoustic phonetics, including very recent ones (Maekawa, 2002).
- Arai, T., “History of Chiba and Kajiyama and their influence in modern speech science,” Proc. of From Sound to Sense: 50+ Years of Discoveries in Speech Communication, 115-120, 2004.
- Chiba, T. and Kajiyama, M., The Vowel: Its Nature and Structure, Tokyo-Kaiseikan Pub. Co., Ltd., Tokyo, 1941.
- Ehrenfest, P., Proc. Amsterdam Acad., 19, 576-597, 1916. (Citation from Schroeder, M. R., J. Acoust. Soc. Am., 41, 1002-1010, 1976.)
- Kent, R. D. and Read, C., Acoustic Analysis of Speech, Singular Publishing, San Diego, CA, 2001.
- Maekawa, K., “From articulatory phonetics to the physics of speech: Contribution of Chiba and Kajiyama,” Acoustical Science and Technology, 23(4), 185-188, 2002.
- Motoki, K., “Three-dimensional acoustic field in vocal-tract,” Acoustical Science and Technology, 23(4), 207-212, 2002.
- Stevens, K. N., Acoustic Phonetics, MIT Press, Cambridge, MA, 1998.
- Stevens, K. N., “The Chiba and Kajiyama book as a precursor to the acoustic theory of speech production,” J. Phonetic Soc. Jpn., 5(2), 6-7, 2001.