ひもの端を持って、スナップをきかせてひもを一振りすることを考えます。すると、ひもには1つの山ができて、それが1つ山の波として進むでしょう。それをイメージしながら次の動画を見てみてください。この動画では手で持っているひもの端が左側にあります。ここで注目していただきたいのは、ひもを表現している点1つ1つが右に移動しているわけではないというところです。どこか1つの点に注目してみましょう(例えば中央付近の赤い点)。その点は波が来た時に、上に位置を変えて最も高い「高さ=1」に達した後、また元の「高さ=0」に戻ります。
ここでもう1つ大事なことを述べます。手を素早く動かして山を作ると、細い山ができます。手をゆっくり動かせば、太い山ができます。ただし、そのいずれであっても波が進む速さは変わりません。媒質が持つ特性によって、波が進む速さが決まるのであって、振動の速さとは関係がないことにご注意ください。
今度は、ひもの端を上下に動かし、単振動をさせてみましょう。次の動画は、そのイメージを表しています。左の端の赤い点を見ると、単振動をしていることが確認できます。そして、結果的にひもには正弦波が伝わっていくことになります。なお、各点の上下の振れは0 → +1 → -1 → 0を繰り返します。このとき、正弦波の振幅は1と表現されます。
ここで、ある瞬間に写真を撮ってみたら、次のようになっていたとします。このとき、山から山までの距離を波長と言い、単位はメートル(m)で表します。
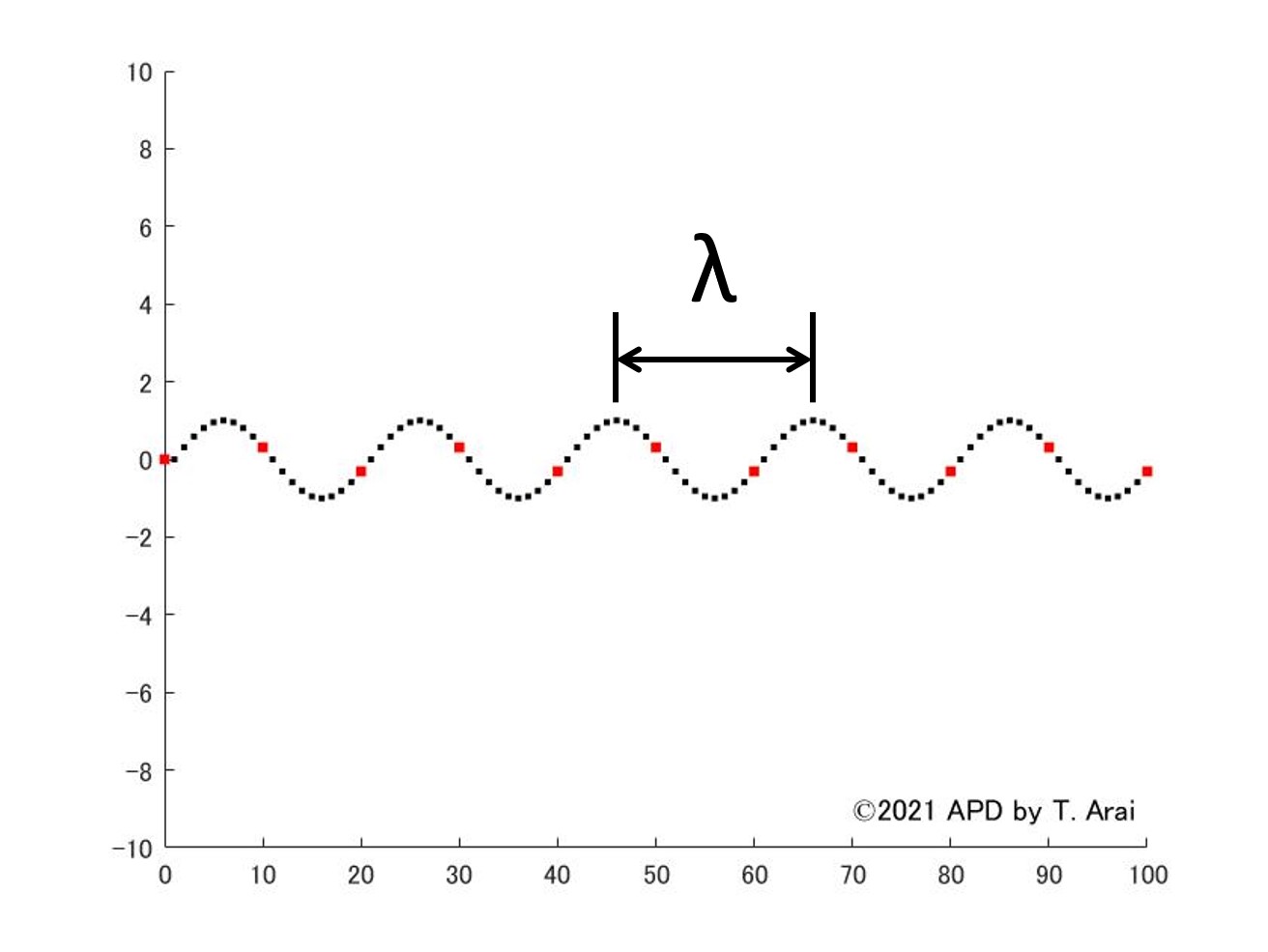
ところで、上では波の伝わる速さと振動する速さの話をしました。振動する速さは振動源によって決まりますが、波の伝わる速さは媒質によって決まります。速さは、距離÷時間で求まりますので、もし波長がλ [m]で周期がT [s]であったら、波の速さvは v = λ / T となります。周期T [s]と周波数f [Hz]の間には逆数の関係があるので、結局、v = λ × f ということになります。
これを言い直すと、波長は波の速さに正比例し、周波数に反比例するということがわかります。波が伝わる速さが速いと波長は長くなり、振動の周波数が低いとやはり波長が長くなります。
ちなみに空気中の音さを例にすると、音さが1秒間に100回振動すれば、音の周波数は100 Hzです。このとき、音波の周期は(1/100より)0.01 sになります。一方、空気中を伝わる音波の速さは、摂氏14℃で約340 m/sです。結局、この音波の波長は(距離=速さ×時間から)約3.4 mということがわかります。