一様音響管において片側が閉じていて、片側が開いている管の場合においても、定常波が形成され、共鳴が起きます。このとき、管の中の空気粒子の速度分布を描いてみると、下の図のようになります。
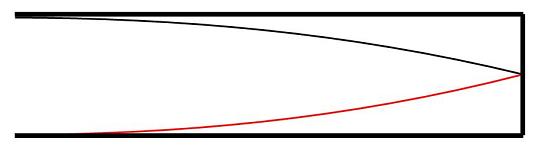
上の図を見てわかるように、閉じている端では節(node)が形成され、開いている端では腹(anti-node)が形成されます。これは、閉じた端では固定端になっている一方、開いている端では自由端になっているからです。このとき作られる音の波長$\lambda$は、管の長さを$l$とすると(上の図の波が波長のちょうど1/4になっているので)$4l$であることがわかります。つまり、
$$\lambda = 4l$$となります。音速を$c$とすると、音の周波数$f$は、
$$f = c /\lambda,$$であることから、
$$f = c / ( 4l )$$となります。もし音速c = 340 m/sで、l = 17 cmの場合、
$$f = c /\lambda = 340 / (4×0.17) = 500\mathrm{Hz}$$すなわち、共鳴周波数が500 Hzになることがわかります。
ところで、この同じ管において次のような定常波もできるので、このときにも共鳴が起きます。
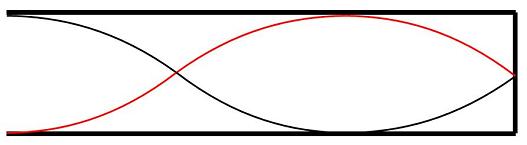
このとき作られる音の波長$\lambda$は、管の長さlに対して4/3倍なっていることがわかります。つまり、
$$\lambda = 4l / 3$$となり、音の周波数$f$は、
$$f = 3c / ( 4l ).$$となります。同様に、
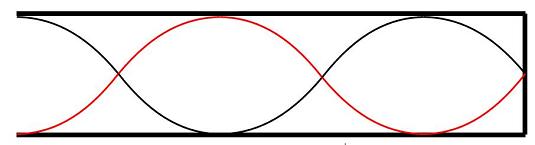
の場合は、
$$\lambda= 4l / 5$$となり、音の周波数$f$は、
$$f = 5c / ( 4l )$$となります。結局、共鳴周波数$f_{n}$は
$$fn = c / ( 4l ) × n \ (n = 1, 3, 5, \cdots)$$となることがわかります。
もし音速c = 340 m/sで、l = 17 cmの場合は、第1から第3共鳴周波数は、500 Hz、1500 Hz、2500 Hzとなります。
ところで、開いている口(開口端)ではその外側の近いところの空気も一緒に振動をします。つまり、実効的な管の長さは実際の管の長さよりも少し長いと考えられます。どのくらい長いかについては管の半径rに依存し、
$$\mathrm{管の実効長} \fallingdotseq l + 0.6r$$となります。管の長さに対してこのような開口端補正を施すことによって、周波数がより正確に求められます。
- Stevens, K. N., Acoustic Phonetics, MIT Press, Cambridge, MA, 1998.