波について、重ね合わせの原理が成り立つといことは、ある波は別の波と波を足し合わせることで表現されることになります。フーリエは、あらゆる波形が正弦波の和として表現されることを教えてくれました(フーリエ変換)。特に、周期的複合音の場合、その時間波形は同じ周期で繰り返す正弦波の和として表現されます。その様子を次の図で見てみましょう。
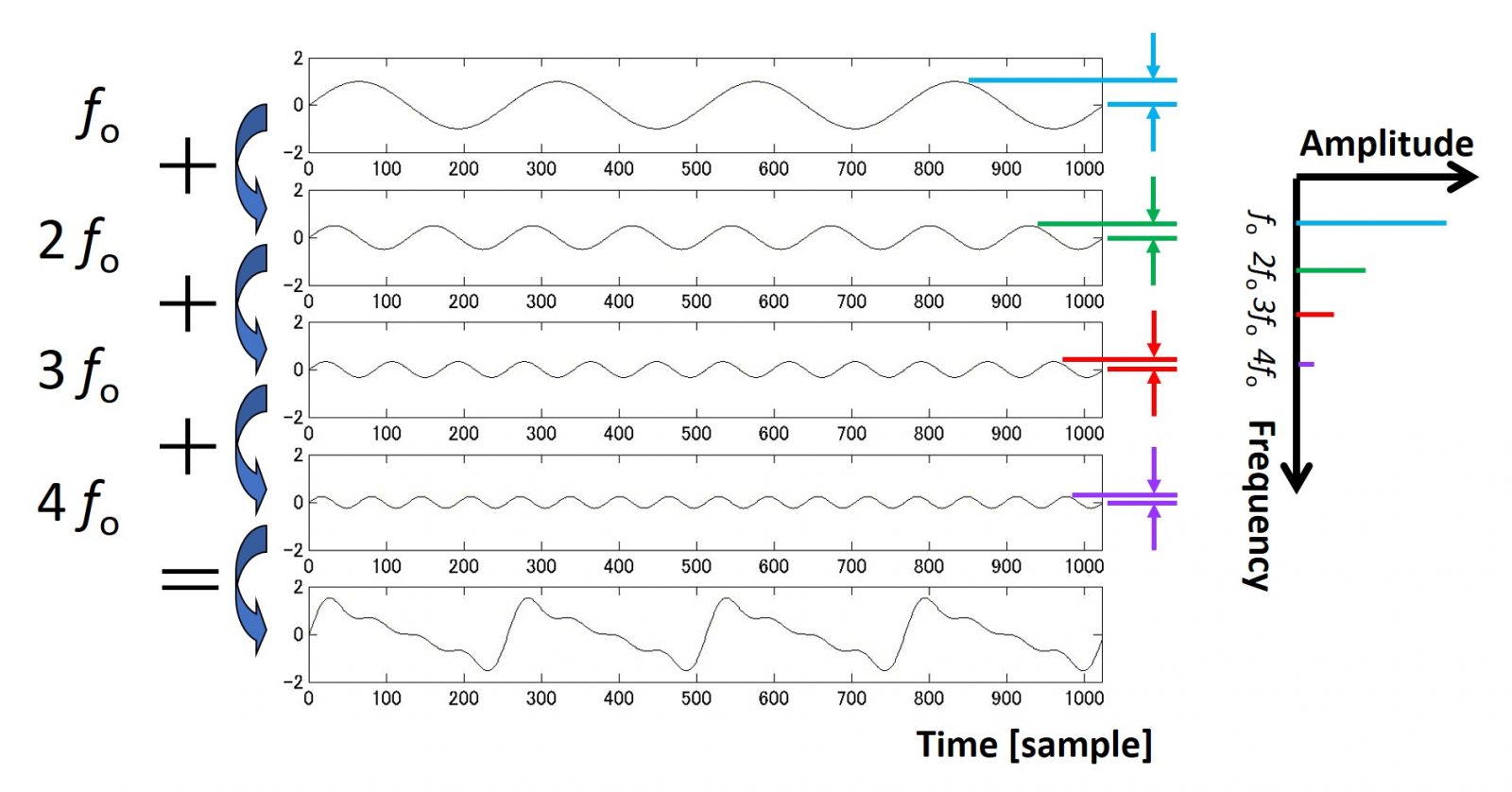
1段目の正弦波(周波数がfo)と2段目の正弦波(周波数が2fo)を比較すると、周波数が2倍になっています。この場合、1段目の正弦波の1周期は2段目の正弦波のちょうど2周期になっています。同様に、3段目は周波数が1段目の3倍(3fo)、4段目は周波数が1段目の4倍(4fo)で、それぞれちょうど3周期と4周期でぴったり1段目の1周期に揃います。ですので、その4つの正弦波を全部足し合わせた一番下の段にある波形は周期的であること、そしてその周期は1段目の周期(これを基本周期と呼びます)と一致します。一番下の段は、周期的複合音の時間波形となっており、構成する4つの正弦波には周波数がfo(これを基本周波数と呼びます)の整数倍になっているという規則があります。
右側に横向きの図が添えられていますが、これは周波数に対する振幅を表しているので振幅スペクトルと呼ばれます。この振幅スペクトルは、4つの正弦波の波の振れ幅を周波数ごとにプロットしたものです。4つの正弦波の周波数は基本周波数foの整数倍であるため、振幅スペクトルはとびとびの周波数に振幅を表す棒が並んだような線スペクトルになります。