母音の声道の形状を単純化していくと、3つの円筒管を接続した「3音響管モデル」として近似されます。その断面の様子を、次の図で示します。
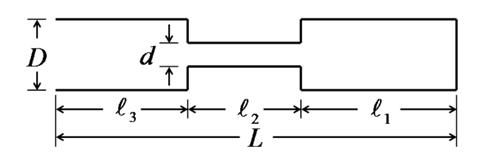
ここで、この声道では右端が喉頭側、左端が口唇側であるとします。また、1つめの音響管は図の一番右で、長さが$l_{1}$、断面の直径が$D$とします。2つめの音響管は図の中央で、長さが$l_{2}$、断面の直径が$d$とします。3つめの音響管は図の左端で、長さが$l_{3}$、断面の直径が再び$D$とします。そして、3つの管を接続したときの全長を$L (= l_{1} + l_{2} + l_{3} )$とします。 もし2つめの音響管の太さ$d$が$D$に比べて十分小さく、それぞれの管における共鳴現象を独立に取り扱うことができるとしましょう。このとき、この管の中で観測される共鳴周波数は、低い周波数において次の3つのものが考えられます。第1は、1つめの音響管における共鳴で、この管は両側が閉じているので、その共鳴周波数は$c / ( 2l_{1})$にて近似されます。第2は、3つめの音響管における共鳴で、この管は片側が閉じて片側が開いているので、その共鳴周波数は$c / ( 4l_{3})$にて近似されます。第3は、1つめと2つめの管によるヘルムホルツ共鳴で、その共鳴周波数は
$$\frac{ c }{ 2 \pi } \sqrt{ \frac{ A_{2} }{ A l_{1} l_{2} }}$$
にて近似されます。ここで、$A$と$A_{2}$はそれぞれ直径がDとdの円の面積で、$A = (\pi / 4)D^2$, $ A_{2} = (\pi / 4)d^2$です。この3音響管モデルでは、各パラメータを適切に選ぶことによって、異なる母音を作り出すことができます。それではそのことを確認するため、「スライド式3音響管モデル」と呼ばれる声道模型を紹介しましょう。この模型は、内径が$D$の外筒の中に、内径が$d$の穴の開いた内筒を挿入し、それをスライドすることによって「狭め」の位置を任意に変えられるような模型です(下図参照)。

この模型において各パラメータを次の図に示す値のように決めて内筒をスライドさせたとき、音響管の共鳴周波数に対する近似曲線を3本の曲線のグラフとして図にして示します。この図では、ヘルムホルツ共鳴に対する共鳴周波数の計算に際し、開口端補正を適用しています。
それぞれの母音のスペクトルを観測すると、共鳴特性が反映されたスペクトルピークとして反映されている様子を見ることができます。このピークはフォルマントと呼ばれ、このピークを低い周波数から順に第1フォルマント、第2フォルマントなどと呼びます。実際に観測されたフォルマント周波数を、図のグラフ中の点として示します。
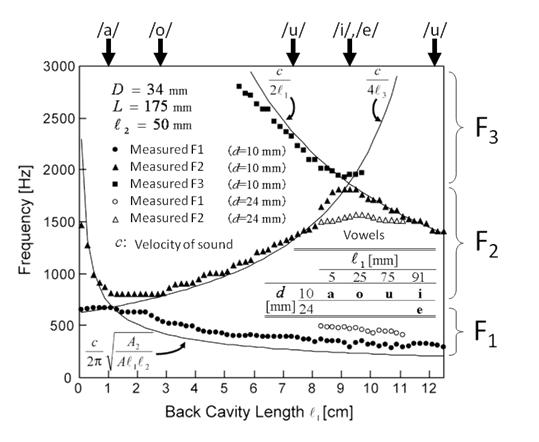
なお、この図では横軸が1つめの音響管の長さ$l_{1}$、縦軸は周波数です。横軸は左が$l_{1}$が短いときですので、狭めが口唇側にある場合に対応します。一方、右が$l_{1}$が長いときですので、狭めが喉頭側にある場合に対応します。この図を見るとわかるように、狭めが後方にあるときは母音の/a/や/o/が、中央付近にあるときに母音の/u/が、前方にあるとき母音の/i/が作られることがわかります。また、母音の/i/と同じ位置で狭めの直径$d$が大きくなると、母音の/e/が作られることがわかります。
- Arai, T., “Sliding three-tube model as a simple educational tool for vowel production,” Acoust. Sci. Tech., 27(6), 384-388, 2006.
- Arai, T., “Education in acoustics and speech science using vocal-tract models,” J. Acoust. Soc. Am., 131(3), Pt. 2, 2444-2454, 2012.
- Fant, G., Acoustic Theory of Speech Production, (Mouton, The Hague, Netherlands), pp. 15-90, 1960.