声道模型 – Arai Laboratory

1. はじめに

我々はこれまで、声道模型として千葉・梶山(1942)[1]に基づく復元を行いました[2]。その声道模型を教材として音響音声学の授業や発声のしくみを示すデモンストレーションなど様々な場面で用いることで、非常に大きな教育的効果を持つことを示してきました[2-20]。

声道模型は、大学や大学院の音声学の授業を始め、音響学、音声言語医学などの分野における音声に関する説明の導入として最適です。特に、声道の形状が母音の音質に関係していること、音源フィルタ理論、パータベーション理論などを説明する際に役立ちます。音声分析ソフトを同時に併用することにより、生成される母音を分析し、そのフォルマント周波数などを確認することも、またその応用の可能性を広げます。そして、この声道模型は大学生以上を対象とするだけでなく、高校生、中学生、さらには小学生までをも対象に、「音声はどのように作られるのか？」を直感的に説明する際の教材として使うことができます。（実際、本声道模型は子供向けの科学館やテレビの科学番組で使われています。）

最初に開発したのは上のようなパイプ型（左）およびプレート型（右）の声道模型ですが、以下ではそれらの紹介と、それを実際の教育現場でいかに活用するかについての応用例をいくつか紹介します。本当の教育効果は声道模型を使ったデモを授業で実際にすることですが、それが出来ない場合でも、以下ではビデオ映像も交えながらより多くの方々に声道模型を使った音響教育の教材を提供したいと思います。そこでは、従来の声道模型をより発展させた頭部形状模型や肺の模型などについても触れます。

2. 母音の基礎

母音が生成される過程は、線形時不変 (linear time-invariant, LTI) システムとしての声道(vocal tract) と、そのシステムに対する入力信号としての声帯音源(glottal sound source) と、放射特性(radiation characteristics)にモデル化できます。（これは母音生成を近似するものであって厳密な表現ではありませんが、多くの場合、非常に良い近似を与えます。）図１はその様子を表しています（図中のsは周波数に対応）。この図において、声帯音源スペクトルU(s)は声道フィルタとしての伝達関数(transfer function) $T(s)$ によってフィルタ処理され、さらに放射特性> $R(s)$ によって高域周波数が強調されて、最終的に $P(s)$ として実際に母音のスペクトルが観測されます。周波数領域において、$P(s)$ は、$U(s)$ と $T(s)$ と $R(s)$ の積によって表現されます。このような母音生成の考え方は、音源フィルタ理論(source-filter theory)[21-25]と呼ばれています。

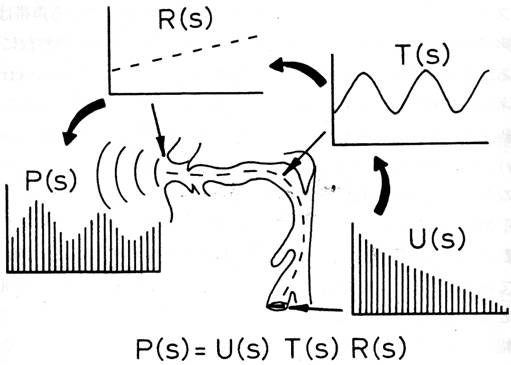
図１に示すように、母音のスペクトルは倍音構造(harmonic structure)をもった線スペクトル(line spectrum)であり、その微細構造の上に声道伝達関数が作る山が包絡線として重畳された形になっています。母音のスペクトル上の山は低い周波数から第1フォルマント（first formant, F1）、第2フォルマント（second formant, F2）、…と呼ばれ、声道の共鳴周波数(resonance frequency)に対応しています。一方、倍音構造は$U(s)$で決定され、音源スペクトルの倍音成分（縦線）の１つ１つの間隔は、音源の基本周波数(fundamental frequency)に対応します。つまり、倍音成分は基本周波数の整数倍のところに存在することになります。

この音源フィルタ理論によると、入力信号（声帯音源）とフィルタ（声道）は独立していると見なすことができます。声帯音源は母音の高さ（ピッチ, pitch）、声質(voice quality)などに関係するのに対し、声道はその形状を変えることによって異なる母音（/a/, /i/, /u/, /e/, /o/など）を作り出すのに関係しています。つまり、例えば高いピッチや低いピッチの母音を作り出そうとした場合、声帯音源の基本周波数のみを変えることによって母音の音質を変えることなく様々な高さの母音を作り出すことができます。

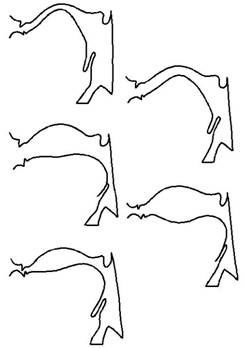
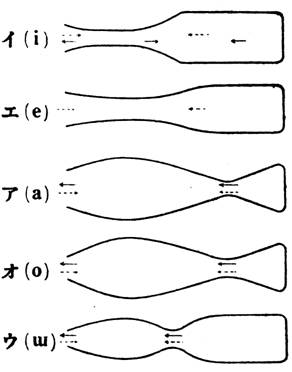
図２. 母音の声道断面図とその形状に対する模式図（文献[1]より、一部改変）

一方、ピッチを変えずに母音の音質だけを変えることも可能です。この場合は、音源の基本周波数を一定にしながら、口の形を大きく開いたり、舌と口蓋の間で狭めを口腔の前方に作ったりするなどによって、例えば/a/や/i/が生成されることになります。図２は日本語5母音の声道断面図と、その形状を大まかに表現した様子を表しています。この図を見ると分かるように、/i/と/e/の場合には（図の左側に相当する）前腔(front cavity)に狭めが存在し、それに比べて（図の右側に相当する）後腔(back cavity)である咽頭腔(pharyngeal cavity)が大きくなっています。一方、/a/, /o/, /u/ではいずれも管の途中に狭めがあります。/a/と/o/では後腔に狭めが存在し、/o/と/u/では口唇付近の開口部も細くなっているのがわかります。

3. 声道模型を使った教育

本声道模型を用いると、声道の形状が母音の音質に関係していること（第3.2節）、そして音源フィルタ理論（第3.3節）を非常に直感的に説明することができます。これはパイプ型、プレート型いずれの型を用いてもそれを示すことができます。特にパイプ型は5母音のデモンストレーションを瞬時に行うのに優れています。一方、プレート型はパイプ型同様、デモンストレーションを行うのにも用いることができる上、学習者が実際に模型を手にとって実験をするのに優れています。さらに、プレート型を用いると、第3.4節に述べるように様々な声道形状を実現することが可能となり、また音声生成におけるパータベーション理論（第3.5節）を体験することが可能となります。以下では、それらの具体的な例を示します。

3.1 音源について

声道模型を使って母音を出すためには、何らかの音源を喉頭側の開口部に入力する必要があります。そのために、ここでは電動式人工喉頭（電気喉頭, electrolarynx）または笛式人工喉頭を用いた例を説明します。

3.1.1 電動式人工喉頭

電動式人工喉頭（以下、電気喉頭）は、喉頭癌などの疾患のため喉頭を摘出した患者さんが、失った声を取り戻すために開発された代用音声のための器具です。電気喉頭自身はブザーのような音しか出すことができません。しかし、喉の側面に振動板を接触させることによって、声帯振動の代わりに電気喉頭の作り出すブザー音が音源となり音声が生成できるようになります。

[デモンストレーション１]

電気喉頭自身、優れた教材となります。実際に、健常者であっても電気喉頭を使って音声生成のデモンストレーションをすることができます。その際、声帯は振動させず、電気喉頭を喉にあて、声道形状を変えながら電気喉頭のスイッチを押すことによっていかにブザー音が「音声のような音」になるかを見せることが可能です。その際、声門を閉じるとより明瞭な音声を生成することができます。

3.1.2 笛式人工喉頭

笛式人工喉頭は電気喉頭と同じ目的で設計された人工喉頭です。ただし、その音の作られ方（ならびに使用方法）が多少違います。電気喉頭の場合、電気的な振動が振動板を叩くことで音が作られていますが、笛式の人工喉頭の場合、発話者による呼気がゴム膜の振動を引き起こして、それが音源となります。

声道模型を用いたデモンストレーションでも、呼気を使って音を作り出すことができます。しかし、場合によっては「呼気を入れている動作」が、見る側には「声を入れている動作」にも見えてしまう可能性があり得ます。したがって以下のように工夫すると、このような誤解を生むことなくより理解の幅が広がるでしょう：

管に呼気を入れる
管にふいごからの気流を入れる
管に膨らませた風船をつける
（以下で述べるような）肺の模型を用いる

3.1.3 肺の模型

人間が音声を発するとき、十分に息を吸ってから吐く呼気を使って音を作ることが一般的です。その「息を吸って吐く」という呼吸のメカニズムからを一緒に示すためには、以下のような肺の模型を使うのが効果的です[26-28]。

[大きい肺のビデオ映像1（818kB）]
[大きい肺のビデオ映像2（1,266kB）]
[小さい肺のビデオ映像（276kB）]

上の図では、左２つが大きな肺の模型（上に乗っているのは、後で述べる頭部形状模型）、右の２つが小さい肺の模型です。いずれも、胸郭を表す容器の下側にゴム膜が張られていて、それが横隔膜を模擬しています。一方、胸郭の中には２つの風船を使って肺が模擬されていて、２又の管を通して容器の上部に開けられた穴から笛式人工喉頭へと接続されています。その先に、さらに声道模型を接続することで音声を出すことが可能となります。

3.2 声道の形状と母音の音質の関係

声道模型を使うと、声道の形状が母音の音質に関係していることを非常に直感的に説明することができます。ここでは、パイプ型声道模型を用いた5母音の生成のデモンストレーションの例を示します。

[デモンストレーション２]

まず電気喉頭だけを取り出し、スイッチを押すことによって電気喉頭自身が作り出す音を再確認します。そのときに、確かにブザー音にしかなっていないことを強調します。続いて、パイプ型声道模型/i/に対してアダプタを介し電気喉頭を押さえつけます。そして、スイッチを入れることによって、先ほどのブザー音が母音/i/になることがわかることを示します。その後、声道模型の種類を変えることによって母音が次々に変化することを示します。その際、それぞれの母音に対し、パイプの形状が以下のような特徴を持っていることも同時に確認していくことが大切です：

母音/i/：前腔に狭めが存在しているのに対し、後腔が大きくなっている
母音/e/：前腔に狭めが存在し後腔が大きくなっているのは/i/と同じだが、/i/よりも狭めが広い
母音/a/：後腔に狭めが存在しているのに対し、口唇側の開口部は比較的開いている
母音/o/：後腔に狭めが存在しているのは/a/に似ているが、口唇側の開口部が細くなっている
母音/u/：声道の中央付近に狭めが存在しているのと同時に、口唇側の開口部も細くなっている

[パイプ型声道模型/i/と小さい肺のビデオ映像（277kB）]
[パイプ型声道模型/e/と小さい肺のビデオ映像（277kB）]
[パイプ型声道模型/a/と小さい肺のビデオ映像（309Bk）]
[パイプ型声道模型/o/と小さい肺のビデオ映像（213kB）]
[パイプ型声道模型/u/と小さい肺のビデオ映像（277kB）]

上記の説明では電気喉頭を使った例を示しましたが、このデモンストレーションでは笛式人工喉頭を用いても同様のことが行えます。また、それぞれの声道模型にアダプタをはめる手間を省くには、場合によっては板状アダプタを用いたほうが素早く次々と母音を変えることができます。

3.3 音源フィルタ理論

音源フィルタ理論によると、音源とフィルタは独立していると見なすことができます。そして、母音のスペクトルは、音源のスペクトルに声道伝達関数、放射特性の積として表現されます。そのことを声道模型を使って、定性的に、あるいは定量的にデモンストレーションする例を以下に示します。

[デモンストレーション３]

ここでは、音源とフィルタが独立しているものと見なすことができることを定性的に説明します。まず、電気喉頭（または笛式人工喉頭）だけの音を聞かせます。その際、特にその音の高さ（ピッチ）がどのように聞こえるかを確認します。次に、各声道模型を通した後の母音がどのように聞こえたかを確認します。ここで強調すべき点は、音源の高さ（ピッチ）がほぼそのまま母音の高さ（ピッチ）になっていること、そして異なる声道模型が異なる母音の音質を生み出しているという点です。音源を電気喉頭から笛式人工喉頭に変えた場合、何が変化するかを問います。そうすることによって、音の高さや声質が音源に支配されていることが確認されます。まとめると、

同じ声道模型を使って異なる音源を入力した場合、同じ母音に聞こえるが音の高さや声質が違うことがわかる
同じ音源を使って異なる声道模型に入力した場合、同じ音の高さや声質に聞こえるが異なる母音に聞こえることがわかる

ということになります。

[デモンストレーション４]

ここでは、実際にスペクトルを求めながら音源フィルタ理論を定量的に理解するデモンストレーションを示します。まず、音源のみによる音を録音し、そのスペクトルを音声分析ソフトを使って求めます。ここで求められるスペクトルは、図１でいうところのいわば $U(s)R(s)$ になります。次に、声道模型を通した後の音を録音し、同様にスペクトルを求めます。このスペクトルは、図１における$P(s) = U(s)T(s)R(s)$になります。２つのスペクトルの違いが、声道伝達関数 $T(s)$ であることがわかります。

[注意事項]

・実際にこれを実行する場合、2回の録音において入力される音源がなるべく同じ必要があります。そのために、電気喉頭の音の出始めから測定して100 msを常に分析の開始位置とし、その時点から20～30 msを分析対象に統一するなど、工夫が必要となります。

3.4 様々な声道形状を実現する

本節では、様々な声道形状を実現し、それを用いたデモンストレーションや実験の例を示します。

3.4.1 単一音響管

もっとも単純な音響管の共鳴現象を説明するには、管の断面積が一様な単一音響管がもっとも基本となります。もし、長さが17 cm程度（男性の声道長の平均的な値）のまっすぐな管があれば、それに電気喉頭などを接続することによって単一音響管による音を作ることができます。

片側が閉じた単一音響管の共鳴周波数は、以下のように求めることができます[21,23,25]。もし、長さ$l = 17$cm、空気中の音速を$c = 34,000$ cm/sとすれば、第１共鳴周波数F1は（1/4波長の共鳴に対応することから）、$$F_{1} = \frac{ c }{ 4l } = 500 \ \mathrm{[Hz]}$$

第２共鳴周波数F2は、$$F_{2} = \frac{ 3c }{ 4l} = 1500 \ \mathrm{[Hz]}$$

以下同様に、F3 = 2500 Hz, F4 = 3500 Hz, …というようになります。このような単一音響管によって作られる音は、中性母音（英語のいわゆる“schwa”）に対応します。

単一音響管に音源を入力すると得られる生成音に対して音響分析を施すと、図１の左端のようなスペクトルが得られることになります。このとき、スペクトル上に現れるピークがフォルマントであり、それらがF1, F2, F3, …となります。

3.4.2 ２音響管モデル

単一音響管を２つ連続させると、共鳴周波数が変わります。母音の/a/や/i/は、そのような2音響管モデルで近似的に表現することが可能です。図３はその様子を模式的に表しています。この場合、右側が閉じていますが、その閉じている側が喉頭側となります。

[デモンストレーション５]

ここでは、プレート型声道模型を使って２音響管モデルに近い声道形状を実現し、実際にその音を確認するようなデモンストレーションを示します。以下のサイズの穴の開いたプレートを順番通りに並べます。ここで、右側が喉頭側、左側が口唇側となります：

穴の直径：38 38 34 34 32 32 32 32 32 16 14 12 12 12 14 [mm]

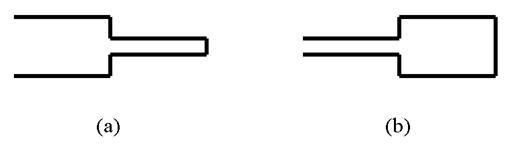
この順番にプレートを並べ、喉頭側（右）から電気喉頭で音源を入力すると、/a/のような母音が生成されるのがわかります。このとき、生成音に対して音響分析を施すと、フォルマント周波数はF1 = 800 Hz, F2 = 1600 Hz付近にあることがわかります。

上記の例は、図３の(a)に相当しました。それでは次に、上記の並びをまったく左右逆にして、図３の(b)に相当する例を考えてみます。これをやはりプレート型声道模型で試してみると、この場合には母音の/i/に近い音になっていることがわかります。つまり、同じ音響管であっても、どちらの端が閉じているかによって共鳴周波数が変わってきます。この場合にも音源を入力し生成音に対して音響分析を施すと、今度はフォルマント周波数がF1 = 300 Hz, F2 = 1800 Hz付近に存在することがわかります。

ところで、上記の図３(b)の状態で口唇側をさらに延長した場合、どのような変化が現れるでしょうか。プレートの配列としては、例えば次のようになります：

穴の直径： 14 10 10 10 12 12 12 14 16 32 32 32 32 32 34 34 38 38 [mm]

これは、いわば「口唇の丸め」を模擬していることになり、生成される音も母音の[y]（ドイツ語のuウムラウト）のような音になることがわかります。

3.4.3 日本語5母音

プレート型声道模型で日本語の5母音を実現する例を以下に示します（右側が喉頭側、左側が口唇側、単位はmm）。

母音
/i/	24	14	12	10	10	10	16	24	32	32	32	32	32	32	12	12
/e/	24	22	22	20	18	16	16	18	24	28	30	30	30	30	12	12
/a/	32	28	30	34	38	38	34	30	26	20	14	12	16	26	12	12
/o/	14	22	26	32	38	38	34	28	22	16	14	16	22	30	12	12
/u/	16	14	20	22	24	26	22	14	18	26	30	30	30	30	12	12

上記のようにプレートを並べ、喉頭側から音源を入力することによって、日本語5母音が生成されます。

3.5 パータベーション理論

パータベーション理論を用いると、音響管の局所的な狭めによって引き起こされる共鳴周波数のシフトを説明することができるようになります[21,25]。ここではその簡単な説明と、プレート型声道模型を用いた実験の例を示します。

それには、まず単一音響管から話を始めます。このような音響管における共鳴現象を考えた場合、各共鳴周波数に対する定在波の状態は体積速度分布によって表現されます。音響管が共鳴していると、ある場所では空気の粒子の振動振幅が最小になり、すなわちそこでは体積速度が最小になることからその点は「節(node)」になります（その場所では圧力は最大）。一方、ある場所では空気の粒子の振動振幅が最大になり、すなわちそこでは体積速度が最大になることからその点は「腹(antinode)」になります（その場所では圧力は最小）。単一音響管では、第１共鳴の定在波は開口端では体積速度が最大（腹）となり、閉じた端では最小（節）となります。第２共鳴では２つの腹と２つの節が存在し、同様に第３共鳴では３つの腹と３つの節が存在します（以下同様に増えていきます）。

一般に、音響管においてその一部に局所的な狭めが存在する場合、共鳴周波数は以下のような法則にしたがってシフトします：

局所的な狭めが最大体積速度（腹）付近にある場合、共鳴周波数は低くなる
局所的な狭めが最小体積速度（節）付近にある場合、共鳴周波数は高くなる

このような共鳴周波数のシフトを模式的に表現したのが図４です。この図では、左側が喉頭側（$x =-l$）、右側が口唇側（$x = 0$）になります。

図4を見るとわかるように、例えば口唇側に局所的な狭めが存在すると、$x = 0$付近ではΔF1もΔF2もΔF3も負のシフト量を示しているように、すべての共鳴周波数が低くなります。局所的な狭めが口唇側より少し内部（前腔の中央付近）に移動すると、ΔF1が負、ΔF2が正になる部分があると思います。そこでは、F1が低くなるのに対してF2が高くなります。

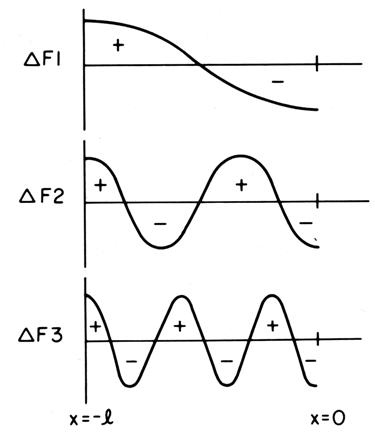
図4. 局所的な狭めが引き起こす共鳴周波数のシフトを表す模式図（文献[25]より）

一方、局所的な狭めが後腔に移動すると、今度はΔF1が正、ΔF2が負になる部分があると思います。そこでは、F1が高くなるのに対してF2が低くなります。このように、パータベーション理論は局所的な狭めによる共鳴周波数の変化の様子を与えてくれます。

[デモンストレーション６]

ここではパータベーション理論によるところの共鳴周波数のシフトを実測することを、プレート型声道模型を用いて試みます。まず、同じ直径で大きめの穴の開いたプレートを複数枚用意し、それによって単一音響管を実現します。そして、局所的な狭めを作るために直径の小さい穴（例えば、10 mm）の開いたプレートを１つ用意します。直径の小さい穴の開いたプレートを口唇側から喉頭側に順番に移動させながら、その都度、フォルマント周波数を測定します。そしてそのフォルマント周波数のシフト量を順番にプロットしていくことによって、図４のようなグラフが得られるはずです。（実際に実測した例が文献[13]にあります。）

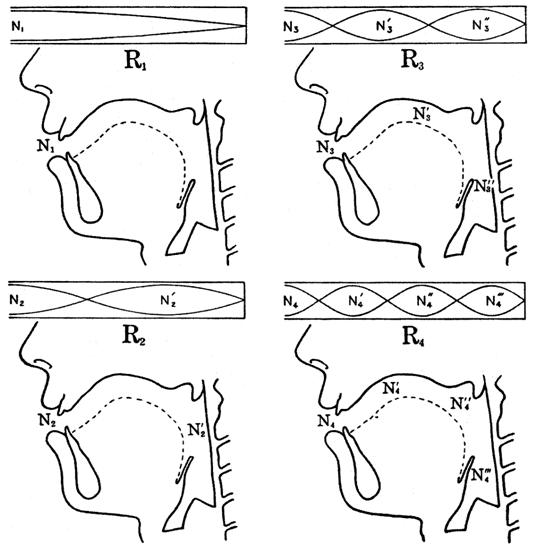
図5. 断面積が一様な単一音響管と声道における体積速度の最大点の分布（文献[1]より）

母音の音質の違いは、図5をもってまとめることができます。図5は、各共鳴モード（F1, F2, F3, F4）における体積速度の分布とその最大点の位置を、断面積が一様な単一音響管と中性母音発話時の声道形状において表しています。F1に対しては、口唇部に最大体積速度の点（N₁）が存在しており、その位置に狭めが起きるとF1が下がります。F2に対しては、口唇部と咽頭部に最大体積速度の点（N₂とN₂’）が存在しており、その位置に狭めが起きるとF2が下がります。また、N₂とN₂’の中間では体積速度が最小になり、その硬口蓋付近に狭めが起きるとF2が上がります。結局、母音/i/では硬口蓋に狭めがあるので高いF2となり、母音/a/では咽頭部に狭めがあるので低いF2となり、母音/u/では口唇部に狭めがあるのでF1もF2も低くなります。

3.6 断面積関数と伝達関数の間における一意性の問題

今までの例を見てきてわかるように、声道断面積関数が決定すると声道フィルタの伝達関数は一意に決まり、したがって入力が与えられればその声道から出力される音は一意に決定します。しかし、逆に音響信号から断面積関数を推定することは単純ではなく、一般に一意に決定することはできません。すなわち、異なる断面積関数を持った２つの声道がまったく同じ伝達関数を持つことがあり得ることになります。以下は、そのデモンストレーションです。

[デモンストレーション７]

次に示す２つのケースについて、4枚のプレートを並べた時に作られる音について両者を比較してみてください：

ケース１）穴の直径： 22 22 22 32 [mm]

ケース２）穴の直径： 22 32 32 32 [mm]

すると、両者とも同じような音の音質を持っていることがわかると思います。これは、異なる断面積関数を持った２つの音響管が同じ伝達関数を持つことを示した例となります。

4. その他の声道模型

4.1 頭部形状模型

まっすぐな声道模型だと、それがどのように頭部に配置されているかがイメージつかみにくい、という欠点があります。それを補うために開発されたのが頭部形状模型です。以下にその頭部形状模型の/i/（左）と/a/（右）を示します。

これらは横から見た写真になっていますが、黒い部分はそれぞれ、母音/i/（左）と/a/（右）を発している時の正中矢状断面を表しています。また、これらの模型はいずれも鼻腔も伴っており、軟口蓋を下げることで鼻咽腔結合を実現することが可能です。大きい肺の模型を使ってこれらの模型から母音の/i/と/a/を発したビデオ映像を以下に示します。

[頭部形状模型/i/と大きい肺のビデオ映像（754kB）]
[頭部形状模型/a/と大きい肺のビデオ映像（850kB）]

4.2 梅田・寺西による声道模型

以下の写真は、梅田・寺西による声道模型を復元したものです。詳しくは、文献[20]をご覧ください。

5. おわりに

パイプ型ならびにプレート型声道模型に関して、音響教育における応用例を示してきました。ここで示したように、本声道模型は、大学や大学院の音声学の授業を始め、音響学、音声言語医学などの分野において、「音声に関する説明」の導入として活用することができます。様々なデモンストレーションを通じて、実際には目にすることのない声道の形状を視覚的に捉えることができますし、また、学習者が実際に模型を手にとって実験したり、実測したりという過程を経ることにより、文字通り、理論を体得することができます。特に、声道の形状が母音の音質に関係していること、音源フィルタ理論、パータベーション理論などを説明する際は、非常に有効です。また音声分析ソフトを同時に併用することにより、生成される母音を分析し、そのフォルマント周波数などを確認することが可能であることも見て参りました。ここでご紹介した応用例はほんの一例ですが、この声道模型が「空気の振動が音を作る」「同じブザー音を使っても声道の形が変わると異なる母音を生み出す」などということを、直感的に伝えることができるという点で、専門的分野に偏らず、まさに子供から大人まで広く楽しめる教材であると信じております。様々な場面で本声道模型がお役に立つことができれば幸いです。