まっすぐに伸びた細い管に息を吹き込むと、「プー」と音がなることがあります。これはその管において、共鳴(resonance)が起きているからです。断面積が一様な(変化しない)管の中における共鳴を見てみましょう。共鳴を起こしているときは、管の中では定常波が形成されています。そのとき、管の中の空気粒子の速度分布を描いてみると、下の図のようになります。
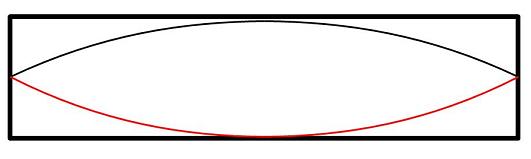
両側が閉じている管の場合、両端で節(node)を形成します。これは、閉じた端では空気の粒子が自由に動けず、固定端になっているからです。
このとき作られる音の波長$\lambda$は、管の長さを$l$とすると(上の図の波が波長のちょうど半分になっているので)$2l$であることがわかります。つまり、
$$\lambda = 2l$$となります。音速を$c$とすると、音の周波数$f$は、
$$f = c / \lambda$$であることから、
$$f = c / (2l)$$となります。もし音速c = 340 m/sで、l = 17 cmの場合、
$$f = c /\lambda = 340 / (2×0.17) = 1000 \mathrm{Hz}$$すなわち、共鳴周波数が1 kHzになることがわかります。
ところで、この同じ管において次のような定常波もできるので、このときにも共鳴が起きます。
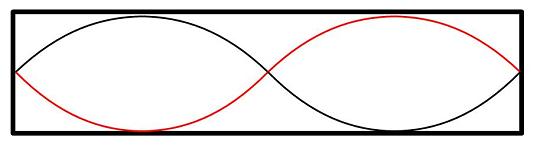
このとき作られる音の波長$\lambda$は、管の長さ$l$とちょうど一致します。つまり、
$$\lambda = l$$となり、音の周波数$f$は、
$$f = c / l$$となります。
同様に、
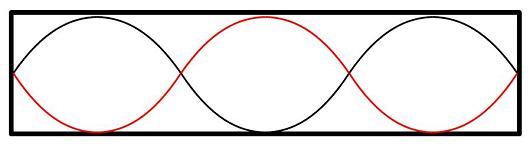
の場合は
$$\lambda = 2l / 3$$となり、音の周波数$f$は、
$$f = 3c / ( 2l )$$となります。結局、共鳴周波数$f_{n}$は
$$f_{n} = c / ( 2l ) × n \ (n = 1, 2, 3,\cdots)$$となることがわかります。
それでは、両側が閉じた一様音響管の中における共鳴現象をKundtの実験によって確認してみましょう。この例では、17 cmの管の中にコルクの粉が入っていて、端にはスピーカが取り付けられています。発振器から周波数が可変の正弦波(純音)を入力すると、ある周波数では音が大きく聞こえ、コルクの粉が「踊る」ところがあります。それが、共鳴周波数に対応します(以下のビデオでは、その周波数は約1kHz)。
- Stevens, K. N., Acoustic Phonetics, MIT Press, Cambridge, MA, 1998.
- Sakamoto, S., Asakura, T., Ueno, K., Sakimoto, Y., Satoh, F. and Tachibana, H., “Visualization of acoustic resonance phenomena using Kundt’s dust figure method,” J. Acoust. Soc. Am., 120(5), 3070, 2006.