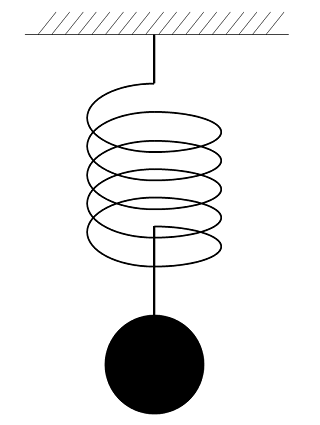
図のように天井からバネを介しておもりを吊り下げることを考えます(バネ・質量系)。このとき、おもりを下に引っ張って離すと単振動を起こします。この様子を少し考えてみましょう。
バネは伸びると縮もうとする力、すなわち復元力が働きます。その力は伸びた長さとおもりの質量に比例します。これはフックの法則(Hooke’s law)と呼ばれます。バネの復元力によっておもりは元の位置(平衡位置)に向かって戻ろうとします。しかし、おもりには慣性があるために平衡位置を通り過ぎて平衡位置よりも高いところにまで到達します。バネは縮むと、同様に伸びようとする復元力が働きます。そして、おもりは最高点から再び下向きに移動を始めます。同様におもりには慣性があるので、平衡位置を通り過ぎて、最下点まで到達し、同じようなサイクルを再び繰り返します。
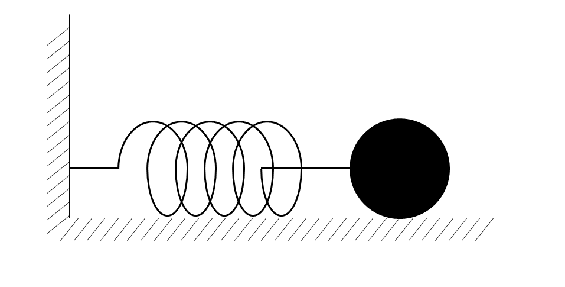
単振動の様子を、エネルギー保存則の観点から見てみましょう。そのために、今度は下の図のように横向きにバネ・質量系がつながれているとします。ここで、おもりは摩擦のない表面を左右に振動するものとします。おもりを右方向の最大位置まで引っ張ってから、離すことを考えます。このとき、右方向の最大位置におもりがあるときは、運動エネルギーは0ですが、弾性エネルギーは最大となります。この後、おもりを離すとバネの復元力によっておもりが平衡位置まで戻ります。このとき、弾性エネルギーは0になりますが、運動エネルギーが最大になります。その後、おもりは左方向の最大位置に到達し、一瞬だけ止まります。このとき、再び運動エネルギーが0になり、弾性エネルギーが最大になります。その後、すぐに今度は右方向に動き出します。そして再び平衡位置に達した際、運動エネルギーは最大となり、弾性エネルギーは0になります。このように、エネルギーが保存される条件の下で、サイクル内において弾性エネルギーと運動エネルギーの間でエネルギーの変換が行われ、それがずっと続きます。
それでは、単振動の周期$T$を求めてみましょう。おもりの質量を$m$、バネのバネ定数を$k$、おもりの平衡位置を0としてx軸を水平方向に取ると、おもりに関する運動方程式は、
$${F} = -{ma} $$ ただし、$a$は加速度です。一方、フックの法則より、
$${F} = -{kx} $$ ここで$x$は平衡位置からおもりがどれだけ変位したか、そしてマイナスの記号はバネによる復元力が逆向きであることを示します。以上の2式から、
$${ma} = -{kx} $$ すなわち、
$${ma}+{kx} = 0 $$ という関係が成り立つことが分かります。ところで、加速度$a$は$x$を時間$t$に関して2階微分したものですので、この式は微分方程式になっています。この微分方程式を解くことによって、おもりが正弦的に振動する解が得られ、その周期$T$は、
$${T} = 2\pi\sqrt{ \frac{k}{m} }$$
結局、周波数$f$はその逆数で、
$$f = \frac{1}{ 2\pi }\sqrt{ \frac{k}{m} }$$
となります。
このような単振動の様子を記録に残すために、おもりにペンを取り付けてみましょう。すると、紙の上をペンの先が描く様子は行ったり来たりする1つの線にしかなりません。しかし、その紙を横にずらしていくと正弦波になる様子が分かります。
音さも同様に単振動を起こします。音さを空気中に置くと、その周りの空気は押されて圧縮されたり、逆に膨張したりを繰り返し、音が縦波として伝搬します。次の図はそのイメージ図を表わしています。音さの周りにおいて、音圧は時間と共に正弦波状に変化します。このような音は純音(pure tone)と呼ばれ、人間にとって単一の音の高さの感覚を与えます。
[References]
- Speaks, C. E., Introduction to Sound: Acoustics for the Hearing and Speech Sciences, Singular Publishing, San Diego, CA, 1999.(荒井隆行, 菅原勉(監訳), 音入門:聴覚・音声科学のための音響学, 海文堂, 2002.)